生成🌲与欧拉公式

欧拉公式
在平面图上
其中
证明
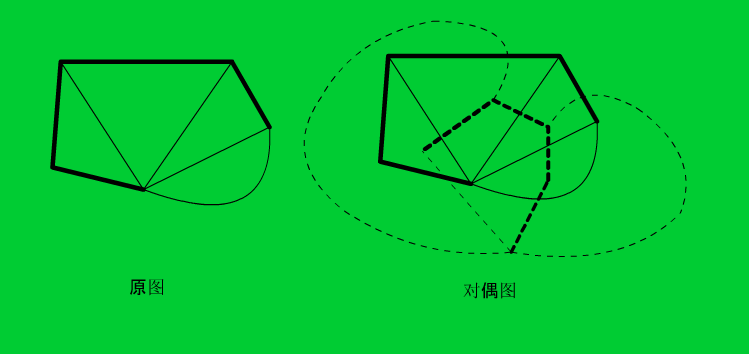
在原图中,先求任意一颗生成树(如图中粗边所标记的),再求出原图的对偶图(如图中虚线所形成的图),即将平面作为点,将相邻的面用边连起来,找出对偶图上那些不与原图中生成树上的边相交的的边(如那些粗虚线标记的)。
首先,粗虚线一定不会吧原图中任意一个点包围,因为每一个点都必须属于原图的生成树,所以此点一定连有有一条边属于生成树,而这条边两边的平面不会连线,所以没有点会被包围。
反过来,生成树也不会吧对偶图上的任意一点包围,所以粗虚线是对偶图上的生成树。
此时,对偶图上有
所以
- Post title:生成🌲与欧拉公式
- Post author:Zheng Yu
- Create time:2016-03-06 13:49:10
- Post link:https://dataisland.org/2016/03/06/euler-formula/
- Copyright Notice:All articles in this blog are licensed under BY-NC-SA unless stating additionally.